Souvent, lorsque j'explique la théorie sartrienne de la liberté, je donne l'argument "l'homme a un potentiel infini", ou, plutôt, je parle de "la faculté infinie de l'homme à changer et se modifier lui-même". Mes amis, en bons scientifiques, me rétorquent alors que ce n'est pas très rigoureux de parler d'infini, parce que l'homme, cela semble indéniable, ne peut pas tout faire. Soit. Mais cet argument ne tient pas, et j'ai définitivement envie d'en finir avec cette notion d'infini.
Donnons un premier exemple. Mettons les concepts physiques de l'infiniment petit et de l'infiniment grand. Ici, l'infini veut dire "extrême", on parle donc de très, très grand. Ce n'est pas parce que quelque chose est très grand que c'est le plus grand, idem pour le petit. De plus, imaginons que nous faisons la taille d'une galaxie, alors, les planètes seront de l'ordre de l'infiniment petit, de même, l'univers, de celui de l'infiniment grand. Ainsi l'infini est-il une notion assez relative au contexte. Je dirais même plus, entièrement solidaire de son contexte.
Ensuite, l'infini, ce n'est pas du tout une notion absolue. L'infini, ce n'est pas quelque chose d'unique. Il est multiple, et je dirai même qu'il y a des infinis plus grands que d'autres. Prenons une approche mathématique (je vais simplifier et expliquer au maximum pour ceux qui n'aiment pas, ne se souviennent pas ou n'ont jamais entendu parler des fonctions) :
On considère deux fonctions simples, les fonctions f et g, et un nombre entier, x. On pose :
f(x) = x et
g(x) = x² + 1.
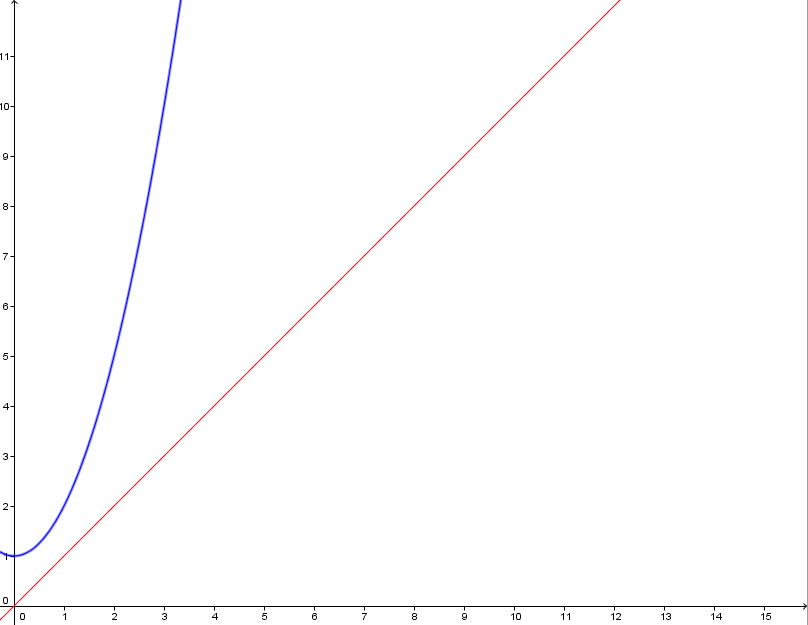
On passe vite sur la partie mathématique un peu formelle, et on trace le graphe des fonctions :
f(x) en rouge, g(x) en bleu.
Ce que l'on remarque de manière très intuitive, c'est que pour le même x, on aura toujours g(x) supérieure à f(x). Et, lorsque x devient très grand, on dit alors qu'il "tend" vers l'infini, et évidemment, f(x) aussi, du coup, tend vers l'infini. Sauf qu'on a g(x) > f(x), donc g(x) tend aussi vers l'infini. Sauf que ce qui est également très intuitif au regard des courbes, c'est que g(x) augmente beaucoup plus vite que f(x). Donc l'infini que g(x) atteint est bien plus grand que celui que f(x) atteint pour un même x. Conclusion, il y a des infinis plus grands que d'autres.
Cela est tout simplement dû au fait que le concept d'infini est très flou. On considère simplement que c'est quelque chose qui ne s'arrête jamais, dans le grand, le petit, le négatif, le beau, le faux, et que sais-je encore. Dans les... potentiels ?
Car voilà où je voulais en venir : l'homme peut faire, de son point de vue, une infinité de choses. Mais du point de vue d'une grenouille, peut-être peut-il faire une plus grande infinité de choses, enfin, cela se discute, et, du point de vue d'une hypothétique espèce plus... avancée technologiquement, logiquement, méthodiquement, au niveau du raisonnement, ou de quelque caractéristique de ce type, voire même du point de vue d'un Être Absolu purement philosophique, et rassemblant une infinité de perfections, et chacune infiniment, alors, cette infinité peut paraître bien plus petite, relativement. Cela dit, cela reste une infinité. Ile existe une infinité de nombres compris entre 0 et 1, comme entre 0 et 2, mais il y en a plus entre 0 et 2 car cet ensemble comprend celui des nombres compris entre 0 et 1. Bref, tout ça pour dire que, malgré le fait que notre potentiel infini puisse être relativisé et surpassé, il reste infini : on peut faire une quantité illimitée de choses différentes. Et surtout, cela ne veut surtout pas dire que l'humain peut tout faire, loin de là...
J'adooore cet article. Ou comment appliquer un raisonnement scientifique à une idée purement philosophique !
RépondreSupprimerC'est là que tu vois que tout est lié. Enfin, pas tout, mais les sciences et la philo le sont intimement. Sans Kant et Descartes, on n'aurait pas la science d'aujourd'hui.
SupprimerQuand à l'idée philosophique d'infini, je pense qu'elle ne prend son sens que définie d'un point de vue strictement et rigoureusement mathématique ^^